*本文是本人于2015年发布游戏开发笔记,当时利用贝塞尔曲线仅在游戏开发领域,文章也仅发布于百度贴吧,没想到数年之后,又可以用在我的爬虫工作上,真是令人感叹,现重新分享出来,提供参考
什么是贝塞尔曲线
先上一段百度百科:贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。在Flash4中还没有完整的曲线工具,而在Flash5里面已经提供出贝塞尔曲线工具。
成品展示
曲线定义
众所周知,gm中可以绘制出各种各样的形状,但却没有曲线绘制,因此功能受到了局限
但是,虽然没有曲线绘制函数,但是gm中却有一种曲线,那就是路径
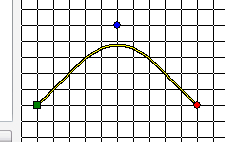
当路径的连接方式设定为平滑曲线时,则绘制出来的路径是一条二次贝塞尔曲线,可以使用draw_path()函数绘制出来
虽然这样可以画出一条曲线,但是由于路径属于资源在使用时不灵活、曲线精度较低、且我们实际使用时大多使用的是三次贝塞尔曲线,因此这种方式不提倡使用
二次曲线看起来就是这样的:
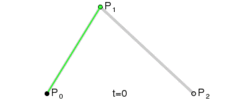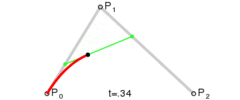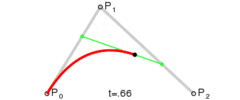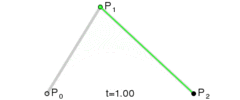
由于我们不使用二次曲线,所以在这里不多加讨论
我们就直接开始讨论三次曲线
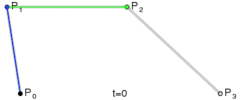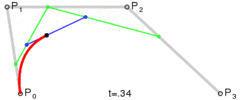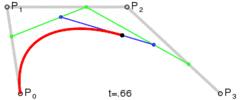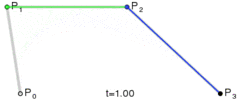
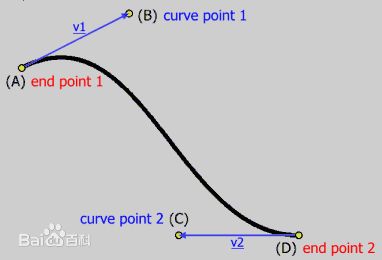
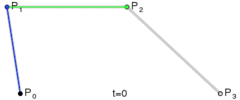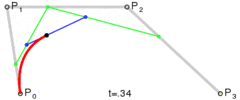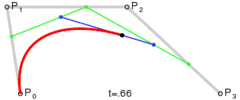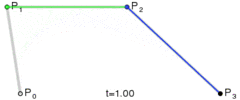
三次贝塞尔曲线比二次曲线多了一个控制点,所以整个曲线由两个控制点(P1,P2)和起始终止点(P0,P3)控制。
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
曲线的参数形式为:
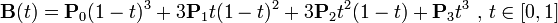
上图的曲线,是参数t从0到1时,上图中移动的黑点所走过的路径,那么看到这里,有些人就不太明白这个三次曲线是怎么定义的了,所以。我们还是得从头说起
三阶贝塞尔曲线是怎么来的
线性贝塞尔曲线
给定点P0、P1,线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出:
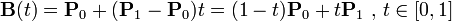
当参数t由0到1变化时,其过程如下:
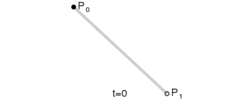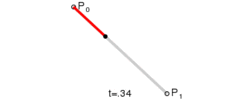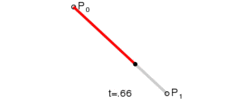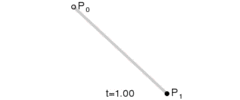
这个t值是曲线占总曲线长度的分量,你可以把总曲线长度看作1,当t为0.5时,图中的黑点就在这条曲线的中间(虽然一次贝塞尔曲线实际上就是条直线)
二次曲线
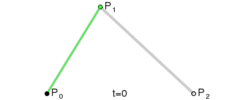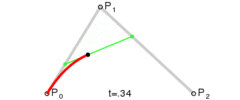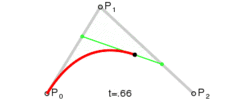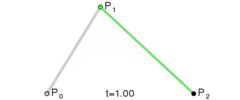
二次曲线实际上是由一次曲线得出的,为构建二次贝塞尔曲线,我们需要定义多条一次贝塞尔曲线
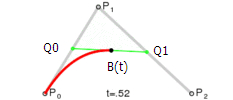
由P0至P1的连续点Q0,描述一条线性贝塞尔曲线。
由P1至P2的连续点Q1,描述一条线性贝塞尔曲线。
由Q0至Q1的连续点Q1,描述一条线性贝塞尔曲线。
由P0至P1的连续点B(t),描述一条二次贝塞尔曲线。
点B(t)所走过的路径就是一条二次贝塞尔曲线
同理,三次贝塞尔曲线也是由多条线性曲线定义的
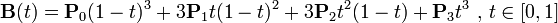
代码实现
那么,知道了原理,我们就能绘制出曲线了,在这里,由于没办法直接绘制曲线,我使用的是原始绘制函数使用多段直线连接的方式绘制出近似曲线
draw_primitive_begin(kind)
//开始一个原始显示类型。
draw_vertex(x,y)
//增加顶点 (x,y)到原始表中,使用之前设定的颜色和透明度 。
pr_linestrip
//一组连续线,从第一个点到第二个点,再到第三个点,等等。最后一个没有 和第一个点连接。你需要指定一个额外的第一顶点拷贝。
draw_primitive_end()
//结束描述原始绘制,这个函数是马上绘制它。用以上代码即可完成连续线的绘制,使用原始绘制直线也比直接用draw_line()+for循环绘制直线要快
我们将他写成一个脚本以便于绘制
///draw_bezier_cubic(x1,y1,x2,y2,x3,y3,x4,y4,complexity);
//画一条三阶贝塞尔曲线 两个控制点(x2,y2,x3,y3) 两个起始点和中间点(x1,y1,x4,y4) 精度(complexity)
var point_x,point_y;
draw_primitive_begin(pr_linestrip)
for(i = 0; i <= 1; i+= 1/argument8){
point_x = power(1-i,3)*argument0 + 3*power(1-i,2)*i*argument2+3*(1-i)*power(i,2)*argument4+power(i,3)*argument6;
point_y = power(1-i,3)*argument1 + 3*power(1-i,2)*i*argument3+3*(1-i)*power(i,2)*argument5+power(i,3)*argument7;
//由曲线函数得出当t==i时的点坐标
draw_vertex(point_x,point_y);
//插入原始绘制顶点,意在将曲线拟合到指定点上
}
draw_primitive_end();
//结束原始绘制,绘制出直线化后的曲线(如果精度足够高,是能达到曲线的效果的)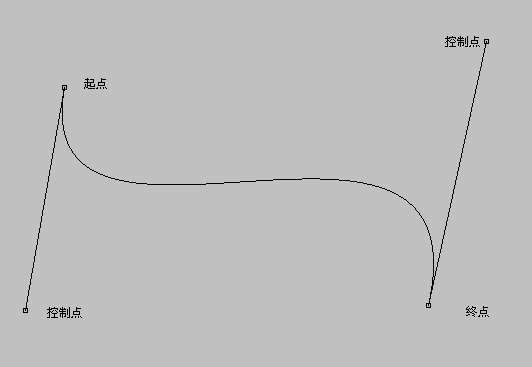
这是精度为100时的曲线,没有直线化的特征

精度为10的曲线,看上去很有意思
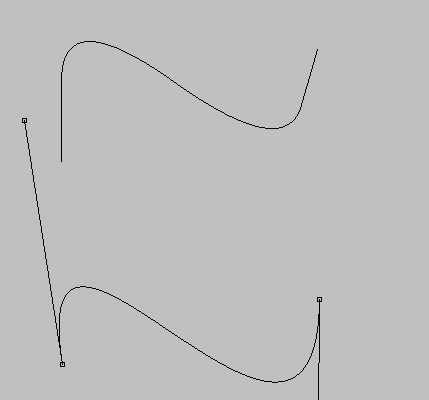
关于这个控制点的绘制,我是用了实例来控制
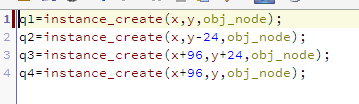
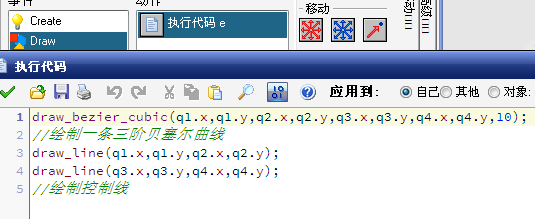
绘制曲线的参数使用的是四个实例的坐标,当我拖动实例时,曲线也会变化
附gmk地址: http://pan.baidu.com/s/1kTzU0lT